
|
Сорок пять запрограммированных частушек о треугольнике |
Частушки-«запростушки» - это только несколько листов, «вырванных» из середины большой ненапечатанной книги «Таблица логарифмов в уме», автором которой является Ф.С. Веснин. Хотя, предлагаемые частушки не являются серьезным источником приобретения знаний, не соответствуют школьной программе, противоречат литературной форме, но все же могут быть использованы учителями на уроках, абитуриентами при подготовке к экзаменам, взрослыми специалистами для углубления своих знаний и неспециалистами для продолжения самообразования, так как «запростушки» запрограммированы на запоминание.
Автор этих частушек Ф.С. Веснин, он не специалист в литературе и стихосложении, а механик, изобретатель, заслуженный рационализатор РСФСР, автор более сотни практических разработок и проектов, касающихся механизации и автоматизации технологических процессов, специализации и концентрации производства, сокращения численности обслуживающего персонала, экономии топлива и электроэнергии. Он лично смонтировал, наладил и пустил в работу несколько сотен единиц оборудования, агрегатов, установок и технологических линий. Он пускал и налаживал в большом историческом интервале всю технику от паровых машин до современных компьютеров.
Ф.С. Веснин задумывал книгу как справочно-познавательное пособие для серьезных взрослых специалистов и руководителей, которые раньше что-то знали, но забыли. Как подсчитать предметы, если их очень много, каков внутренний объем аппарата, если определить его размеры невозможно, какую нагрузку выдержит двутавровая балка, как рассчитать подачу сверла на станке и т.д. Ответы на эти и многие другие вопросы в форме запрограммированных частушек можно найти в книге «Таблица логарифмов в уме».
|
| Частушки – «запростушки» о треугольнике и его элементах |
- Площадь треугольника по основанию и высоте.
- Формула Герона (площадь треугольника по трем сторонам).
- Радиус вписанной в треугольник окружности.
- Радиус описанной около треугольника окружности.
- Радиусы внешние.
- Площадь треугольника по четырем радиусам.
- Площадь треугольника по углам и радиусу описанной окружности.
- Площадь треугольника по одной стороне и трем углам.
- Площадь треугольника по двум сторонам и углу между ними.
- Площадь равностороннего треугольника по стороне.
- Площадь прямоугольного треугольника по гипотенузе и острому углу.
- Площадь прямоугольного треугольника по гипотенузе и сумме синусов.
- Площадь равностороннего треугольника по квадрату основания.
- Измерение площади треугольника линейкой.
- Деление треугольника пополам.
- Деление треугольника пополам.
- Площадь треугольника по его средней линии.
- Деление гипотенузы высотой.
- Пересечение гипотенузы с высотой.
- Высота прямоугольного треугольника.
- Высота равностороннего треугольника.
- Высота треугольника по радиусу вписанной окружности.
- Радиус вписанной окружности по высоте треугольника.
- Высота треугольника, вписанного в окружность.
- Радиус окружности, описанной около треугольника.
- Высота любого треугольника.
- Сторона вписанного в треугольник квадрата.
- Квадрат биссектрисы треугольника.
- Биссектриса треугольника.
- Деление стороны треугольника биссектрисой.
- Квадрат медианы треугольника.
- Третья часть оси и медианы треугольника (см. 41).
- Радиус окружности, вписанной в прямоугольный треугольник.
- Радиус окружности, вписанной в треугольник.
- Треугольник наименьшего периметра, вписанный в треугольник.
- Радиусы вписанной и описанной окружностей для правильного треугольника.
- Две окружности в треугольнике.
- Три окружности в треугольнике.
- Квадрат межцентрового расстояния.
- Теорема Пифагора.
- Окружность Эйлера.
- Площадь треугольника на сфере.
- Площадь треугольника по координатам вершин на плоскости.
- Площадь треугольника по координатам вершин в пространстве.
- Координаты центра тяжести треугольника, многоугольника и многогранника.
|
1) Площадь треугольника по основанию и высоте.
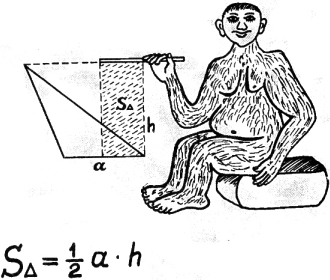
Площадь треугольника
знали предки те,
что пол основания
брать по высоте.
|
24) Высота треугольника, вписанного в окружность.
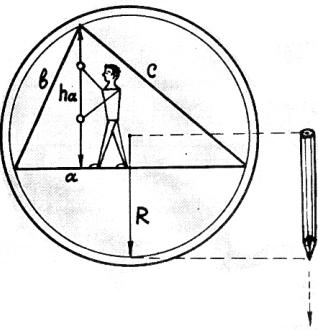
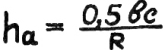
Опять в кольце
высотомер.
Ноль-пять «бэ-цэ» делить на «эр».
|
2) Формула Герона (площадь треугольника по трем сторонам).
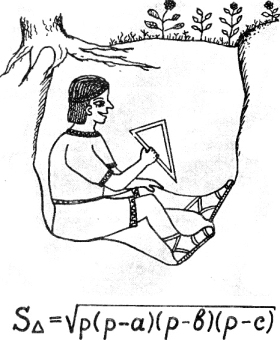
Герон полупериметр
под корень затащил,
Три раза перемножил
и площадь получил.
|
25) Радиус описанной окружности.

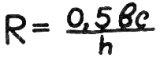
Берите снова карашдаш,
ноль-пять «бэ-цэ»
делить на «аш».
|
3) Радиус вписанной в треугольник окружности.
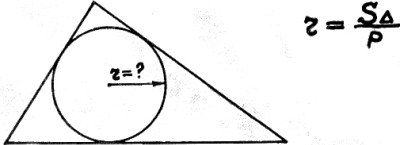
Если площадь треугольника
на полупериметр разделить,
то самый малый радиус
нетрудно получить.
|
26) Высота любого треугольника.
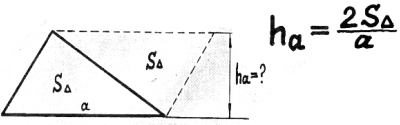
Высоту у треугольника
легко определить,
если брать двойную площадь
и на сторону делить.
|
4) Радиус описанной около треугольника окружности.
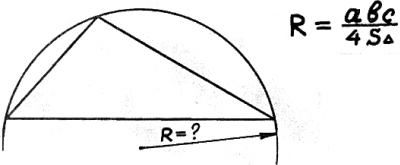
Как радиус побольше
аbс-олютно сбыть?
На четыре площади
надо разделить.
|
27) Высота вписанного квадрата.
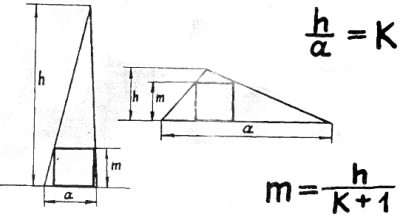
Надо «аш» делить на «а»
и обозначить буквой «ка».
Высота будет сейчас:
«аш» делить на «ка-плюс-раз».
|
5) Радиусы внешние.

И радиусы внешние
будут нам видны,
когда разделим площадь
на полупериметр
без этой стороны.
|
28) Квадрат биссектрисы.
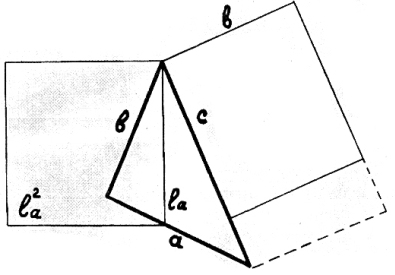
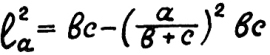
Квадрат биссектрисы
На сторону «а»:
«бэ цэ» минус скобка,
в числителе «а»,
внизу «бэ-плюс-цэ»,
после скобки квадрат,
и «бэ цэ» биссектрису
узнать очень рад.
|
6) Площадь треугольника по четырем радиусам.
Все радиусы внешние
и внутренний один
для вычисленья площади
под корень поместим.
|
29) Длина биссектрисы.
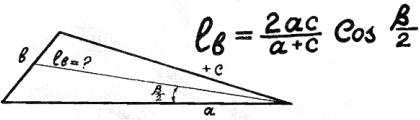
Поселились во дворце
дробь «два-а-цэ»
на «а-плюс-цэ»,
ко-синус «бэта-пополам» -
биссектриса, значит там.
|
7) Площадь треугольника по углам и радиусу описанной окружности.
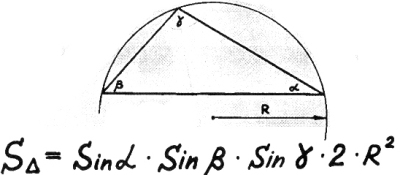
Мы площадь треугольника
запишем в длинный ряд,
перемножив синусы
на два, на «эр-квадрат».
|
30) Деление стороны треугольника биссектрисой.
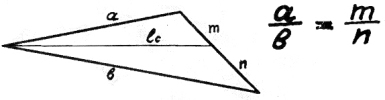
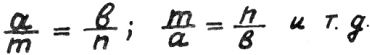
Биссектриса делит угол,
также сторону в глуши.
Прилегающие стороны
В пропорцию впиши.
Пропорции вращаются,
крест-накрест умножаются,
у нас о том частушка есть,
она не забывается.
|
8) Площадь треугольника по одной стороне и трем углам.
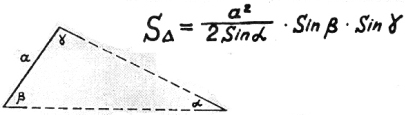
«А-в-квадрате» разделяем
на два синуса своих
и еще перемножаем
на два синуса других.
|
31) Квадрат медианы.
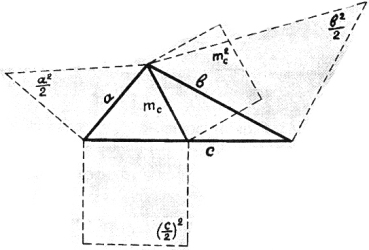
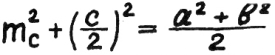
Квадрат медианы
и полстороны –
полсуммы квадратов
с другой стороны.
|
9) Площадь треугольника по двум сторонам и углу между ними.
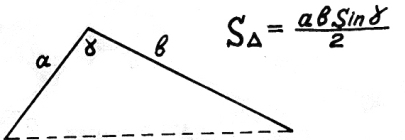
«А» на «бэ» на синус «гамма»
разделили пополам,
снова площадь получили,
повезло, конечно, нам.
|
32) Третья часть оси и медианы.
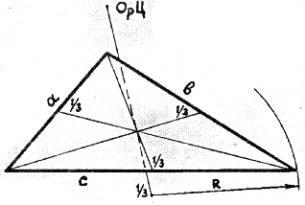
Медиана отделяет
третью часть сама собой,
когда встретится на линии
с подругой дорогой.
|
10) Площадь равностороннего треугольника.
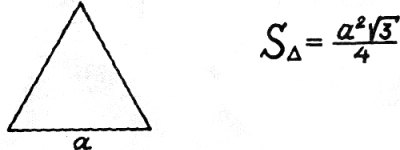
«А-квадрат»
на корень трех
и делить
на четырех.
|
33) Радиус окружности, вписанной в прямоугольный треугольник.
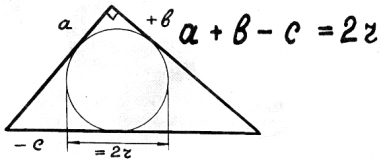
«А» плюс «бэ»
и минус «цэ»
напиши «два-эр»
в конце.
|
11) Площадь прямоугольного треугольника по гипотенузе и острому углу.
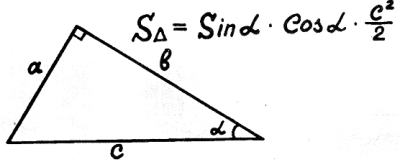
Прямоугольный треугольник
подарили нынче нам:
альфа, синус на ко-синус,
«цэ-квадрат» напополам.
|
34) Радиус вписанной окружности любого треугольника.
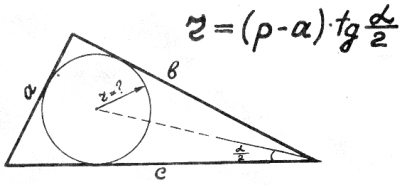
«Пэ-без-а»,
скажу я Вам,
на тангенс
«альфа-пополам».
|
12) Площадь прямоугольного треугольника по гипотенузе и сумме синусов.
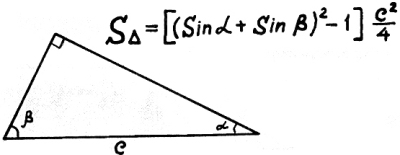
От суммы синусов в квадрате
единицу отнимать,
а квадрат гипотенузы
на четыре разделять.
|
35) Вписанный треугольник наименьшего периметра.
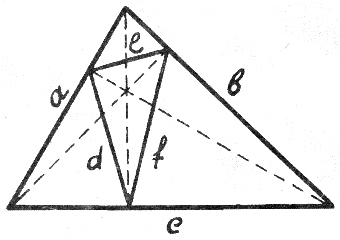
Наименьшим по периметру
конечно, будет тот,
у которого вершины
в основаниях высот.
|
13) Площадь равностороннего треугольника по квадрату основания.
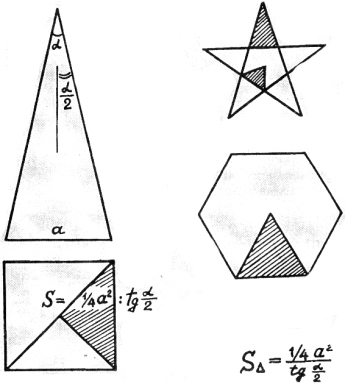
Квадрата четверть
делишь сам
на тангенс
«альфа-пополам».
|
36) Радиусы правильного треугольника.
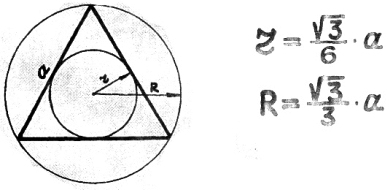
Малый радиус там есть:
корень трех делить на шесть,
и большой там посмотри:
корень трех делить на три.
|
14) Измерение площади треугольника линейкой.
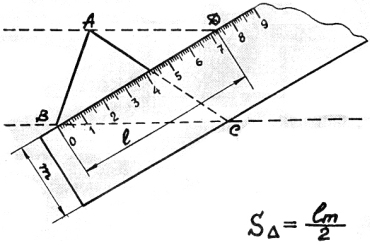
Очень точной быть должна
у линейки ширина.
Шириною закрываем
от угла и до угла (В и С),
параллель еще проводим (АД)
от свободного угла (А).
На деление линейки (Д)
она кажет. Стало быть,
остается перемножить
и на двойку разделить.
Но ведь можно же шкалу
в гектарах градуировать,
чтоб по карте все поля
просто интегрировать.
|
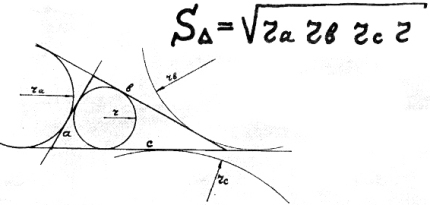
37) Два круга в треугольнике.
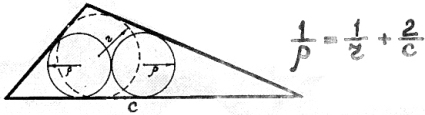
Эти радиусы будем
буквой «ро» обозначать
и такую формулу
можем написать:
«один-дрбь-ро»
равно в конце
«один-дробь-эр»
плюс «два-дробь-цэ».
|
15) Деление треугольника пополам.
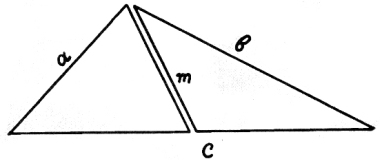
Медиана для того
служит в треугольнике,
чтобы надвое его
делили наши школьники.
|
38) Три круга в треугольнике.
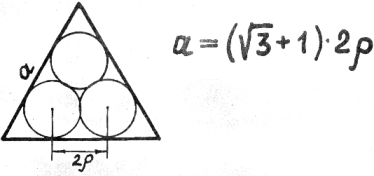
Сторона нам пригодиться.
вычисляем не хитро:
корень трех плюс единица
умножаем на «два-ро».
|
16) Деление треугольника пополам.
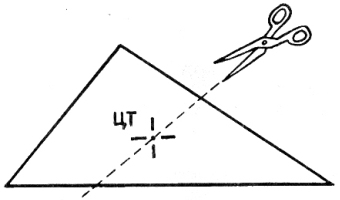
Если резать треугольник
через центр тяжести,
то всегда напополам
разрезать придется Вам.
|
39) Квадрат межцентрового расстояния.
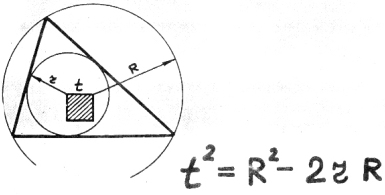
«Два-эр-на-эр»
надо отнять
от «большого
эр-квадрат».
|
17) Площадь треугольника по его средней линии.
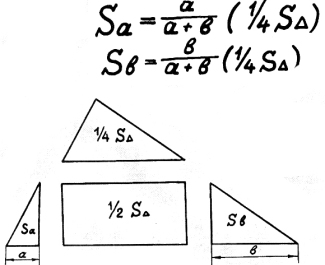
По средней линии отрежем
четверть площади. Потом
выкроим прямоугольник –
половина будет в нем.
Остаются два кусочка.
Их площадь надо знать тебе?
то «а» делить на «а-плюс-бэ»
и «бэ» делить на «а-плюс-бэ».
Эти доли четвертинки
Можешь вырезать себе.
|
40) Теорема Пифагора.
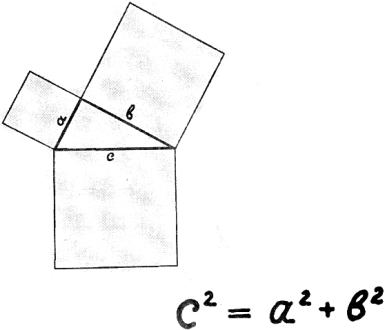
В прямоугольном треугольнике
названия сторон:
гипотенуза и два катета
известны с тех времен.
Что квадрат гипотенузы
равен сумме, так сказать,
квадратов катетов, конечно,
это, братцы, надо знать.
Это, братцы, надо знать
и теорему Пифагора
никогда не забывать.
|
18) Деление гипотенузы высотой.
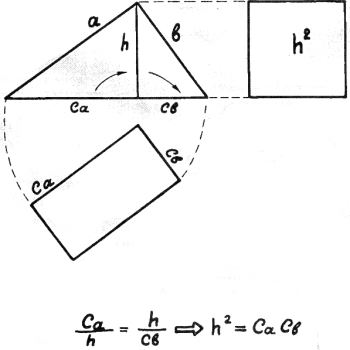
Высота гипотенузу
делит по пропорции:
часть большая к высоте,
как высота к «пол-порции».
|
41) Окружность Эйлера.
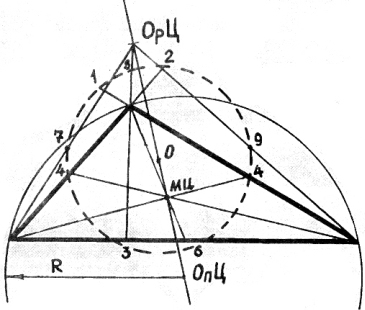
На одной прямой лежат
Три центра треугольника:
«опицентр»,
«медицентр»,
«ортоцентр»,
Известно будет школьникам.
Между крайних посредине
центр окружности одной,
на которой девять точек
расположены давно:
основания высот (1,2,3),
середины всех сторон (4,5,6),
середины от вершины (7,8,9)
к ортоцентру
знает он.
|
19) Пересечение гипотенузы высотой.
Высотой гипотенуза
так пересекается,
что квадрат гипотенузы
на два распадается.
|
42) Площадь треугольника на сфере.
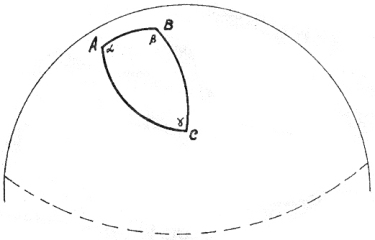
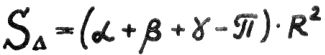
На сфере треугольник.
Избыток по углам
на «эр-квадрат» умножим
и площадь скажем Вам.
|
20) Высота прямоугольного треугольника.
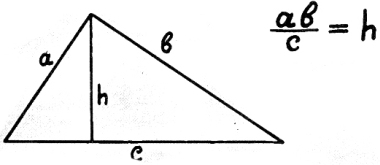
«А-на-бэ»
делить на «цэ»
высоту писать
в конце.
|
43) Площадь треугольника по координатам вершин на плоскости.
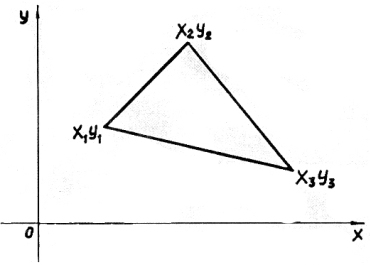
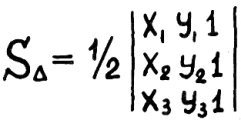
Икс, игрек, единица
три раза записать
и пол-определителя
в ответ надо сказать.
|
21) Высота равностороннего треугольника.
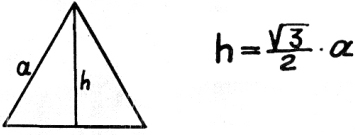
Высота равностороннего
давно известна нам:
корень трех берем в числителе
и делим пополам.
|
44) Площадь треугольника по координатам вершин в пространстве.
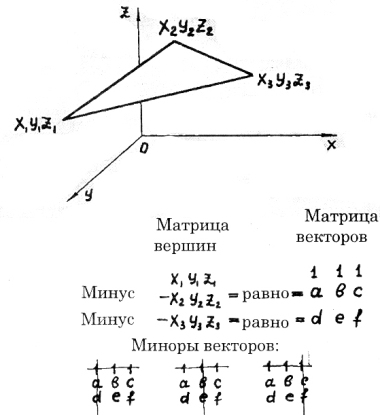
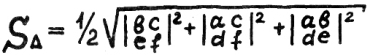
Вершины матрицей запишем,
по ним два вектора найдем,
сверху пишем единицы,
миноры их в квадрат берем.
От суммы этих трех квадратов
полкорня будем находить,
чтоб треугольника в пространстве
площадь сразу сообщить.
|
22) Высота треугольника по радиусу вписанной окружности.
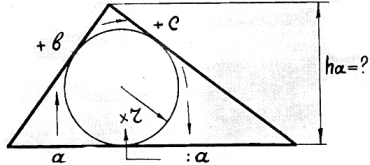
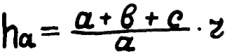
«А» плюс «бэ» плюс «цэ» сперва
разделить на букву «а».
Разделили?
А теперь
умножать на малый «эр».
|
45) Координаты центра тяжести треугольника, многоугольника и многогранника.
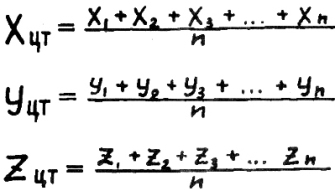
Координаты центра тяжести
легко определить:
арифметическое среднее
по каждой находить.
|
23) Радиус вписанной окружности по высоте треугольника.

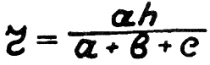
«А-аш» обратно,
стало быть,
на периметр делить.
|
|





