Спортивный класс

В классе 38 человек. Из них 16 играют в баскетбол, 17 - в хоккей, 18 - в футбол. Увлекаются двумя видами спорта - баскетболом и хоккеем - четверо, баскетболом и футболом - трое, футболом и хоккеем - пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом.
Сколько ребят увлекаются одновременно тремя видами спорта?
Сколько ребят увлекается лишь одним из этих видов спорта?
Решение.
Воспользуемся кругами Эйлера.
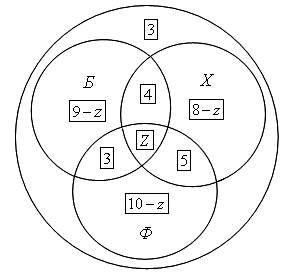
Пусть большой круг изображает всех учащихся класса, а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов.
Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта.
Из рассмотрения кругов Эйлера видно, что одним лишь видом спорта -
баскетболом занимаются
16 - (4 + z + 3) = 9 - z;
одним лишь хоккеем
17 - (4 + z + 5) = 8 - z;
одним лишь футболом
18 - (3 + z + 5) = 10 - z.
Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам:
3 + (9 - z) + (8 - z) + (10 - z) + 4 + 3 + 5 + z = 38,
z = 2.
Таким образом, двое ребят увлекаются всеми тремя видами спорта.
Складывая числа 9 - z, 8 - z и 10 - z, где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек.
Ответ.
Двое ребят увлекаются всеми тремя видами спорта человека.
Увлекающихся лишь одним видом спорта: 21 человек.
| 




